Desde la antigua Grecia hasta el diseño digital moderno, la proporción áurea revela cómo un simple número —1.618— conecta matemáticas, naturaleza, arte, música y percepción humana, desdibujando la frontera entre ciencia y armonía

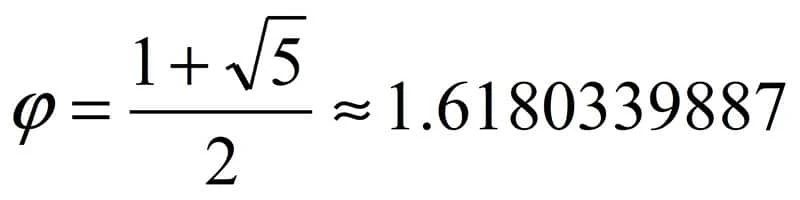
Por El Ingeniero S

Código Beta

Existe un numero que ha maravillado a la humanidad desde tiempos de la antigua
Grecia: el número Phi, también conocido como el número áureo. Phi es una cifra
que resulta de dividir entre dos la suma de uno mas la raíz de cinco (=1.618...
con infinitos decimales). Phi ha fascinado a matemáticos, y también a artistas,
biólogos, músicos, arquitectos, historiadores y psicólogos porque representa la
belleza y la singularidad del arte y la naturaleza.

Antes de contar la historia, importancia e impacto de este número, haremos una
pequeña encuesta. En la figura gráfica se muestran cinco diferentes rectángulos
que tienen el mismo perímetro -suma de los cuatro lados- pero con diferente
longitud y anchura. ¿Cuál es rectángulo que te gusta más?

Revisemos las proporciones de lado mayor sobre el lado menor en cada rectángulo: 4 opción 1, 3 opción 2, 2.3 opción 3, 1.6 opción 4, y 1.2 opción 5. Ahora, es muy posible que tu respuesta sea el rectángulo 4, con una proporción del de 1.6. Escogiste el rectángulo áureo que se basa en el número phi. Vamos a revisar porque este número se considera mágico. No dejes que las matemáticas y fórmulas que presentare te desanimen a leer todo este artículo. A phi solo hay que admirarlo.

Aspectos históricos fundamentales

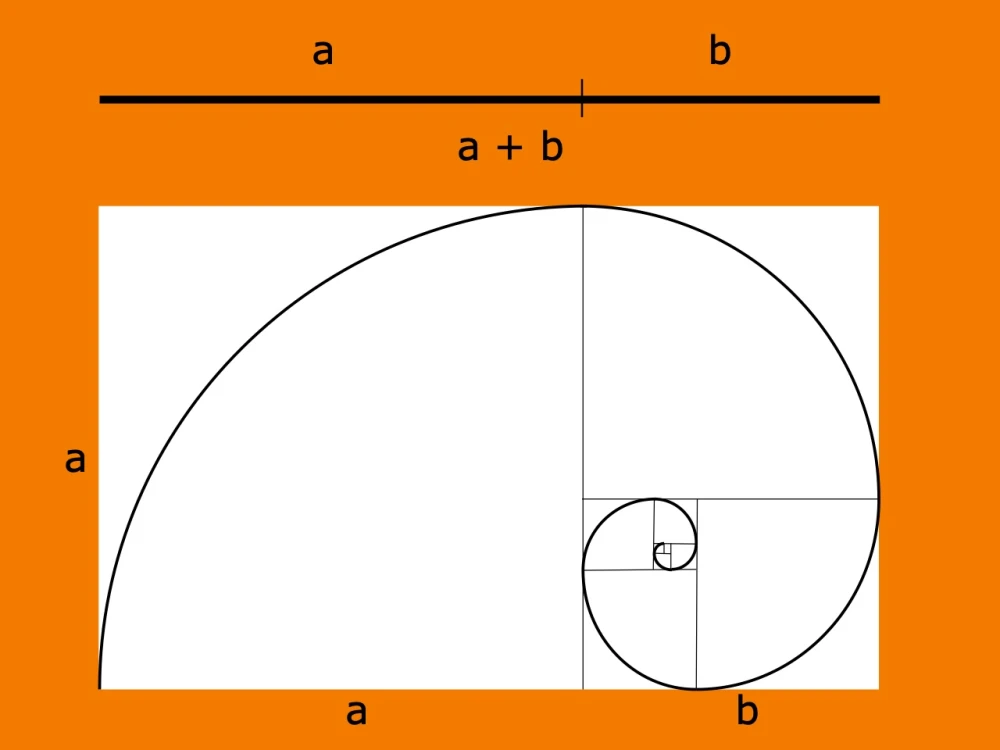
El descubrimiento de este número en la antigua Grecia es crucial. Los pitagóricos ya conocían la proporción, pero Euclides la formalizó en “Los Elementos” (300 a.C.) como “división en media y extrema razón”. Si un segmento de longitud a+b se divide en dos partes desiguales, obteniendo los segmentos a y b, en un punto donde se cumpla la condición de que el segmento a+b es al segmento mayor a lo que éste al lado menor b. La razón o cociente en ambos casos es la misma y es la que se conoce como el número phi: (a+b)/a = a/b = φ =1.618…

La denominación “número áureo” o “proporción áurea” tiene esa historia fascinante de cómo diferentes culturas la valorizaron. El término “phi” fue introducido en el siglo XX en honor al escultor griego Fidias, a quién se le atribuyen las esculturas del Partenón de Atenas.

El mundo Maya notó que había patrones espirales especiales en algunas semillas (como el girasol). Se especula que en la Edad Media el mundo Oriental conoció esta proporción, y una vez que los números indo-arábigos, incluyendo el cero -lo que entonces carecía de sentido para la iglesia-, se introducen al Occidente por FIbonacci en el siglo XIII, el número phi fue redescubierto durante el Renacimiento, cuando Luca Pacioli escribió “La Divina Proportione” (1509), con ilustraciones de Leonardo da Vinci, estableciendo su conexión con la belleza divina.

Propiedades matemáticas

El número phi (φ) se define como φ=(1+√5)/2. Phi es un número irracional, o sea, que no puede expresarse como una fracción de números enteros. Asimismo, φ es el número irracional “más irracional” porque tiene la peor aproximación por fracciones, lo que matemáticamente lo hace único. Aquí está lo realmente especial: phi es el único número donde φ² = φ + 1. Precisamente ésta simple ecuación es la base de la proporción áurea. 

La Potencia Exponencial es una Suma 

Una de las características más raras de φ es que para elevarlo al cuadrado, no necesitas multiplicar; solo tienes que sumarle 1. Esta propiedad se extiende a potencias superiores, permitiendo expresar cualquier potencia de φ cómo una combinación lineal de φ y 1:

φ² = φ + 1

φ³ = φ² + φ = (φ + 1) + φ = 2φ + 1

φ⁴ = 3φ + 2

φ⁵ = 5φ + 3

Nota curiosa: ¿Te fijas en los coeficientes (1, 2, 3, 5...)? Son exactamente los números de la Sucesión de Fibonacci. Su conexión con la sucesión de Fibonacci es espectacular: la razón entre números consecutivos de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21…) converge hacia phi (13/8=1.625, 21/13 ≈1.615). Es un puente hermoso entre la aritmética básica y una constante irracional.

El Inverso es una resta

Si divides toda la ecuación original por φ, obtienes una propiedad única en el mundo de los números:   1 / φ =  φ - 1  Esto significa que para hallar el recíproco de φ, solo tienes que restarle 1. El valor de φ es aproximadamente 1.618, por lo tanto, su inverso es 0.618. Tienen exactamente la misma parte decimal.

Revisa este video para que te quede más claro el concepto del número áureo y sus derivados.

Presencia en la naturaleza

El número phi, en forma de la espiral áurea y ángulo áureo (137.5 grados), y su relación con la secuencia Fibonacci se presentan en la naturaleza. Algunos ejemplos verificables incluyen: la disposición de pétalos en flores (girasoles con sus espirales de Fibonacci); La filotaxis en plantas (cómo se distribuyen las hojas para maximizar luz solar); las proporciones en conchas nautilus y caracoles; las estructuras de huracanes y galaxias; y los patrones en piñas de pino y alcachofas. Aunque algunos de estos ejemplos populares son aproximaciones al número phi, no hay ciertamente exactitudes.

Sin embargo, la aparición de la proporción aérea y las secuencias Fibonacci en los ejemplos selectivamente mencionados son un reflejo de patrones fundamentales en el crecimiento y empacado, ya que obedecen a una mejor eficiencia lograda empacando semillas u optimizando el acceso a luz solar (hojas). También algunos organismos crecen añadiendo partes nuevas en proporción a las existentes, lo que lleva a formar espirales. 

El siguiente video explica la espiral de Fibonacci y el ángulo áureo.

Impacto en arquitectura y artes visuales

Tradicionalmente se ha creído que el El Partenón es el ejemplo clásico del uso del phi en la arquitectura, aunque ahora se debate esa idea ya que las proporciones del templo en realidad son aproximaciones a la proporción áurea.

Más verificable es el uso consciente de phi en el Renacimiento, ya que, por ejemplo, Leonardo Da Vinci lo incorporó en muchas de sus obras, destacando el hombre de Vitrubio. Posteriormente, Le Corbusier desarrolló su sistema “Modulor” basado explícitamente en phi para diseño arquitectónico.

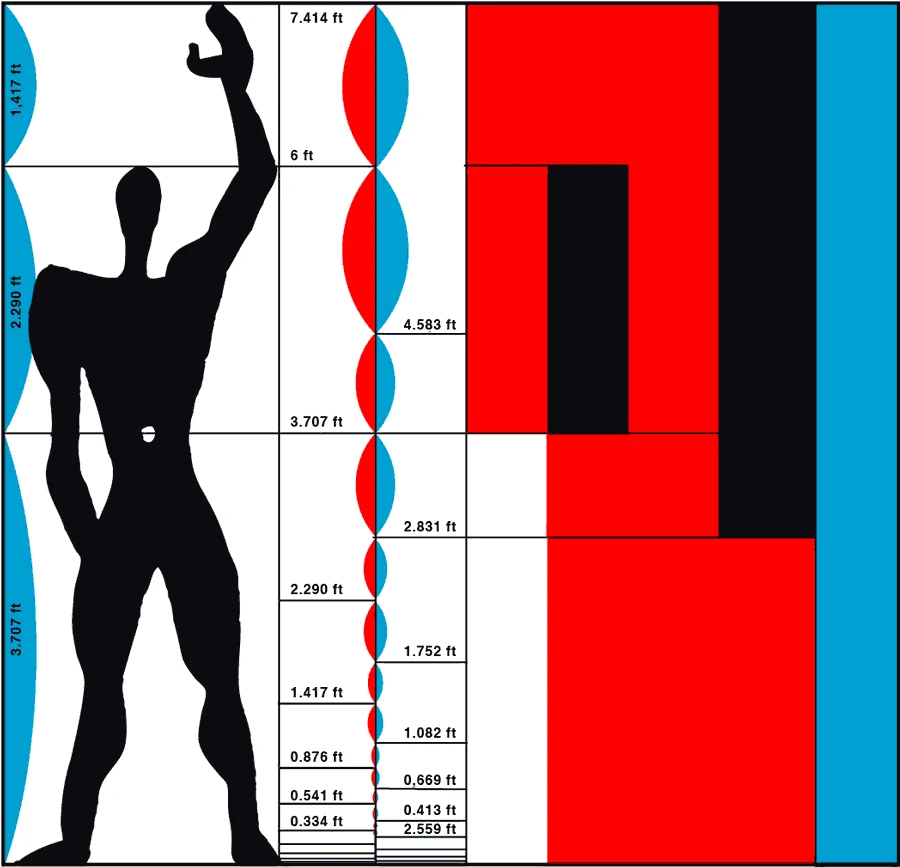
Salvador Dalí utilizó conscientemente rectángulos áureos en “Sacramento de la Última Cena”.

Piet Mondrian, en su búsqueda de armonía universal, empleó estas proporciones en sus composiciones abstractas.

Música y humanidades

Algunos musicólogos encuentran la proporción áurea en obras de Bach, Mozart, Beethoven y Debussy (La Mer), particularmente en la ubicación del clímax y las transiciones. Por ejemplo, la sonata para piano K. 330 de Mozart muestra momentos significativos (desarrollo/recapitulación) alrededor de la barra 62 en un movimiento de 100 barras. Bartók conscientemente empleó la sucesión de Fibonacci en composiciones como Música for Cuerdas, Percusión y Celesta en su movimiento de apertura con el solo del Xilófono. 

La música pop moderna también lo utiliza. En muchas canciones populares, el momento más intenso o memorable —un solo, un cambio de ritmo o el clímax final— suele aparecer cerca del 62% de la duración total del tema. La canción de Lady Gaga “Perfect Illusion” presenta un significativo cambio de clave al segundo 111 del total de 179 segundos, alineándose a la proporción áurea (179/111≈1.618). 

No porque los músicos hagan cálculos matemáticos, sino porque esa distribución del tiempo resulta especialmente satisfactoria para el oído humano. Cuando una canción “crece” de forma progresiva y alcanza su punto culminante ni demasiado pronto ni demasiado tarde, nuestro cerebro percibe la estructura como natural y equilibrada.

En literatura, algunos análisis encuentran estas proporciones en la estructura de obras clásicas, aunque esto es más especulativo.

El mito versus la realidad

Debemos reconocer que hay una “fiebre del número áureo”. Hay muchas afirmaciones populares (rectángulos áureos en tarjetas de crédito, logos corporativos) que son pseudocientíficas. La tendencia humana a encontrar patrones puede llevarnos a “descubrir” phi donde no existe intencionalmente.

Estudios psicológicos sobre preferencias humanas por rectángulos áureos tienen resultados mixtos. Algunos experimentos sugieren una leve preferencia, otros no encuentran nada concluyente. Desde el siglo XIX se ha estudiado phi en el contexto de estética y percepción visual. Esos experimentos sugirieron que la gente tiene una preferencia natural por el rectángulo áureo sobre otras formas geométricas.

Investigación neurocientífica moderna sugiere que el cerebro pudiera procesar patrones del número áureo más eficientemente. Por otro lado, aunque la simetría se ha considerado como un predicador universal de la belleza, la relación áurea frecuentemente es vista como una “orden mayor de simetría” que crea armonía visual y equilibrio, tales como la proporción del ancho de la boca-nariz o el espaciado de los ojos. 

Toda esta fiebre por la proporción áurea se ha minimizado por investigaciones recientes (2024), que no encontraron evidencia que vincule a la proporción áurea con las proporciones ideales del humano o a su belleza facial, notando que los estándares varían significativamente entre culturas. 

Aplicaciones contemporáneas

La proporción áurea se utiliza para crear composiciones naturalmente placenteras en diseño digital, fotografía, y diseño de interfaces. Frecuentemente se visualiza con el patrón phi, que tiene la líneas más cerca del centro que la regla de tercios, guiando a los ojos hacia puntos de interés para balancear imágenes dinámicas y funcionando bien en objetos con curvas o en movimiento.

Cierre filosófico

La proporción áurea basada en el número phi ha fascinado a la humanidad desde civilizaciones milenarias hasta la antigua Grecia y el Medio Oriente. Desde Platón hasta Kepler. Desde el Renacimiento hasta nuestros días. ¿Por qué? El número phi representa la intersección entre matemáticas, naturaleza, arte y percepción humana. Es un ejemplo de cómo patrones matemáticos subyacen a fenómenos diversos, sugiriendo un orden profundo en el universo.